MNAR(Missing Not At Random)データが推薦モデルの学習・オフライン評価に与える影響
映画の例:データの説明1
映画の例で、MNARデータがオフライン評価に与える影響について考えてみる. \(u \in {1，...，U}\)をユーザidx、\(i \in {1，...，I}\) を映画idxとする.
![]()
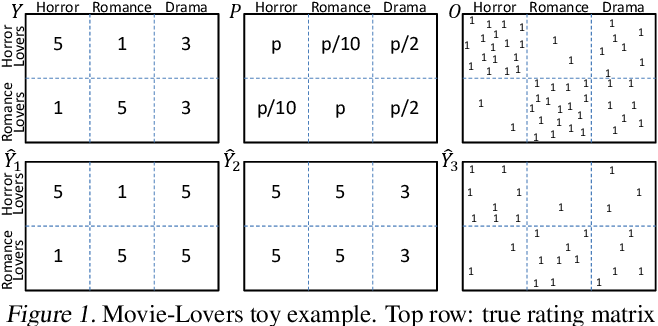
- 図1 左上の\(Y\)は、“ホラー好き”ユーザ集合は全てのホラー映画を5点、全てのロマンス映画を1点と評価する(“ロマンス好き”ユーザ集合は逆)様な真の評価行列 \(Y \in \mathbf{R}^{U \times I}\)
映画の例:データの説明2
![]()
- 図1 右上のbinary行列 \(O \in \{0, 1\}^{U \times I}\) は実際に評価が観測された{u,i}ペア. \([O_{u,i} = 1] ⇔ [Y_{u,i} \text{observed}]\) を意味する. (\(O\)はobservationの意味)
映画の例:データの説明3
![]()
- 図1 中央上の行列 \(P\)は、各{u,i}の評価が実際に観測される確率 \(P_{u,i} = P(O_{u,i} = 1)\) を意味する. この映画の例では、映画ジャンルの好き嫌いと評価値の観測されやすさに強い相関がある.
映画の例:データの説明4
![]()
- 図1の左下 \(\hat{Y}_1\) と中央下 \(\hat{Y}_2\) は、ある推薦モデル1と2によって予測された評価行列を表す.
今回の例では、推薦モデルによって予測された評価行列 \(\hat{Y}\)が，真の評価行列\(Y\)をどれだけ予測できるかを推定(評価)したい…!
推薦モデルの予測誤差の推定:真の予測誤差関数
標準的な予測誤差の場合、次のように書くことができる. (学習の場合は損失関数として、オフライン評価の場合は精度指標として使用するイメージ…!)
\[
R(\hat{Y}) = \frac{1}{U \cdot I} \sum_{u=1}^{U} \sum_{i=1}^{I} \delta_{u,i}(Y, \hat{Y})
\tag{1}
\]
ここで、\(\delta_{u,i}(Y, \hat{Y})\) は真の値 \(Y\) と予測値 \(\hat{Y}\) の差を表し、具体的な \(\delta()\) 関数は採用するmetricによって異なる. 例えば MSE と accuracy の場合は以下.
\[
MSE: \delta_{u,i}(Y, \hat{Y}) = (Y_{u,i} - \hat{Y}_{u,i})^2
\\
Accuracy: \delta_{u,i}(Y, \hat{Y}) = \mathbf{1}(Y_{u,i} = \hat{Y}_{u,i})
\]
推薦モデルの予測誤差の推定:naive推定量
しかし実環境では真の評価行列\(Y\)は一部の要素しか観測されない為、従来は以下の様に、観測済み要素{u,i}のみを用いて 予測誤差 \(R(\hat{Y})\) を推定する.
\[
\hat{R}_{naive}(\hat{Y})
= \frac{1}{|{(u,i):O_{u,i} = 1}|} \sum_{(u,i):O_{u,i}=1} \delta_{u,i}(Y,\hat{Y})
\tag{5}
\]
ここで、\(O_{u,i}\) は観測されたか否かを表すbinary確率変数とする.
\[
E_{O}[O_{u,i}] = P(O_{u,i} = 1)
\]
式(5)を、予測誤差 \(R(\hat{Y})\) のnaive推定量と呼ぶ. 実はこのnaiveさが、図1の \(\hat{Y}_1\)、\(\hat{Y}_2\) に対する重大な誤判定を招いてしまう.
推薦モデルの予測誤差の推定:naive推定量のbias
予測誤差 \(R(\hat{Y})\) のnaive推定量の期待値を導出して、biasの発生を確認します!
\[
E_{O}[\hat{R}_{naive}(\hat{Y})] = E_{O}[\frac{1}{|{(u,i):O_{u,i} = 1}|} \sum_{(u,i):O_{u,i}=1} \delta_{u,i}(Y,\hat{Y})]
\\
= E_{O}[\frac{1}{|{(u,i):O_{u,i} = 1}|} \sum_{(u,i)} O_{u,i} \cdot \delta_{u,i}(Y,\hat{Y})]
\\
\because O_{u,i} \text{は観測されたか否かを表すbinary変数}
\\
= \frac{1}{|{(u,i):O_{u,i} = 1}|} \sum_{(u,i)} E_{O}[O_{u,i}] \cdot \delta_{u,i}(Y,\hat{Y})
\]
(参考: 施策デザインの為の機械学習入門)
推薦モデルの予測誤差の推定:naive推定量のbias
\[
E_{O}[\hat{R}_{naive}(\hat{Y})] = \frac{1}{|{(u,i):O_{u,i} = 1}|} \sum_{(u,i)} E_{O}[O_{u,i}] \cdot \delta_{u,i}(Y,\hat{Y})
\]
この導出結果から、naive推定量の期待値 \(E_{O}[\hat{R}_{naive}(\hat{Y})]\) は、ある特殊ケースを除いて、真の予測誤差 \(R(\hat{Y})\) に比例しない事が分かりました…!
特殊ケース: 全ての観測ペア(u,i)の観測されやすさ(観測確率)が一様なケース:
\[
E_{O}[O_{u,i}] = const \in (0, 1] , \forall {(u,i):O_{u,i} = 1}
\]
↑はまさにデータがMAR(Missing at Random)であるケース. (しかし前述した選択バイアスの影響により、実サービスで得られるデータは多くの場合MNAR…)
そして \(E_{O}[O_{u,i}] = P(O_{u,i} = 1)\) なので、naive推定量は観測されやすい{u,i}ペアに関する誤差を重視する様な設計になっている.
MNARデータのbiasを何とかするアプローチ達
MNARデータを推薦モデルの学習 & オフライン評価に使う上で、大きく3種のアプローチがあるらしい.(参考:論文2より)
- なんとかMARデータを収集する. “forced rating approach”(強制評価アプローチ)と呼ばれる方法. (i.e. ユーザに評価してくれと協力をお願いする方法)
- MNARデータのbiasを補正できるように、モデルの真の予測誤差の不偏推定量となるような新しい推定量を設計する.
- MNARデータからデータをサンプリングし、MARデータに近い性質を持つ介入テストデータを作る.
- (今回読んだ論文2つ目はこっちに該当. LINEさんはオフライン評価時にこちらを採用してるとの事.)
読んだ論文1: 推薦システムにおけるMNARデータを使った学習 & 検証において、因果推論の傾向スコアを用いて誤差関数を調整する事でbiasに対処する論文
詳しくは、元論文か、別途まとめたスライドにて.
提案手法の概要①
予測誤差関数のnaive推定量が”観測されやすさ”に関するbiasを含むと分かったので、予め、“観測されやすさ”の逆数で{u,i}を重み付けしておく様な IPS(Inverse Propensity Score)推定量を設計しよう! それを学習時の損失関数やオンライン評価時の精度指標に使おう！って話.
\[
\hat{R}_{IPS}(\hat{Y}|P) = \frac{1}{U \cdot I} \sum_{(u,i):O_{u,i} = 1} \frac{\delta_{u,i}(Y, \hat{Y})}{P_{u,i}}
\\
= \frac{1}{U \cdot I} \sum_{u} \sum_{i} \frac{\delta_{u,i}(Y, \hat{Y})}{P_{u,i}} \cdot O_{u,i}
\\
\because \text{O_{u,i}はbinary変数なので...!}
\]
ここで、\(P_{u,i} = P(O_{u,i} = 1)\) は 嗜好データ \(Y_{u,i}\) を観測する傾向(propensity) と呼ぶ. (因果推論の文脈では、control群/treatment群に割り当てられる確率=傾向スコア(propensity score)の意味合いが一般的な印象🤔)
提案手法の概要②
予測誤差のIPS推定量 \(\hat{R}_{IPS}(\hat{Y}|P)\) の場合、推薦モデルの学習 or オフライン評価時に、傾向スコア(propensity score) \(P_{u,i} = P(O_{u,i} = 1)\) が必要.
推薦システムの運用方法に応じて、以下の2種類の設定がある:
- Experimental Setting: “観察パターンの生成メカニズム”が推薦システムの制御下にある設定. (ex. 広告配信システムは、どの広告をどのユーザに見せるかを完全に制御している.)
- -> 開発者にとって \(P_{u,i}\) は既知.
- Observational Setting: 観察パターンの生成メカニズムの一部にユーザの意志が含まれる設定. (ex. 映画のオンライン配信では、ユーザが視聴する映画をユーザ自身が選ぶ.)
- -> 開発者にとって \(P_{u,i}\) は未知. 別途、\(P_{u,i}\) を推定する必要がある.
傾向スコア推定モデルの活用(シンプルなやつだけ!)も紹介していました.
実験結果の概要① MNARデータを使った推薦モデルのオフライン評価における提案手法の効果は?
表1は、\(\alpha = 0.25\) (=かなりMNARなデータ)の場合のMAEとDCG@50の推定値の結果.(行:各推薦モデル, 列: 真の値 及び 各推定量による予測誤差)
![]()
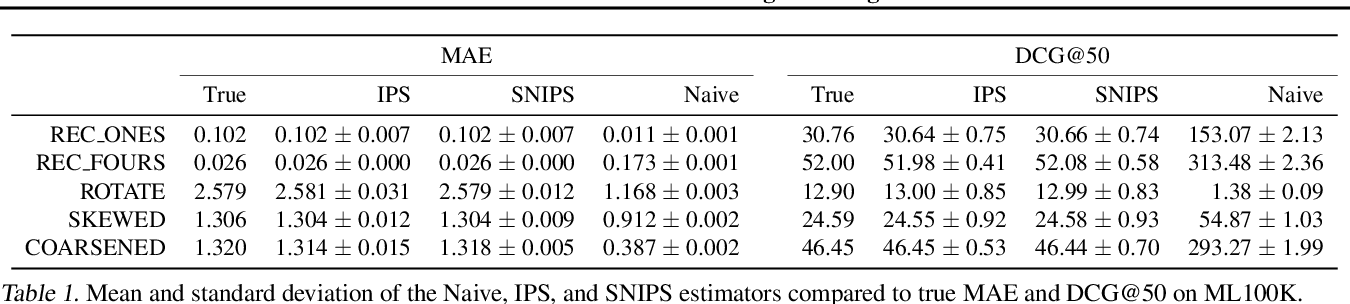
- IPS推定量の平均値は、MAEとDCGの両方で真の性能に完全に一致する.
- naive推定量は著しく偏り、推薦モデルの良し悪しの誤ったランク付けを導く.(ex. REC ONESの性能をREC FOURSよりも高くランク付けしてしまう.)
実験結果の概要② MNARデータを使った推薦モデルの学習における提案手法の効果は?
MCARデータとMNARデータの両方を含んだベンチマークデータセットにおいてMNARデータを使って推薦モデルを学習させ、提案した損失関数の性能を評価した. 表2は、MCARテストセットに対する予測精度を評価したもの.
![]()
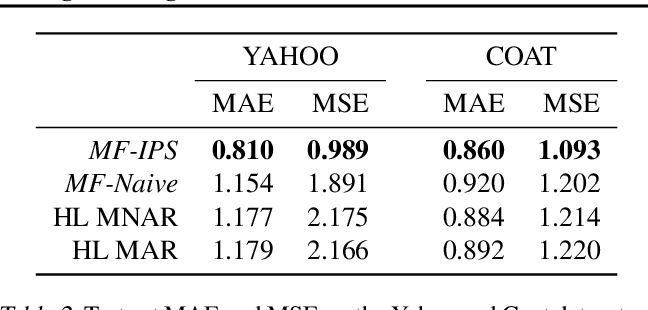
MF-IPSは、MF-naiveや既存debias手法(HL-MNARやHL-MAR)を大幅に上回った. 更にMF-IPSの性能は、YahooデータセットのSOTAに近い結果だったとの事.
読んだ論文2: MNARデータを使った推薦モデルのオフライン評価において、データを重み付けサンプリングしてMARデータに近づける事でbias軽減を試みる論文
詳しくは、元論文か、別途まとめたスライドにて.
提案手法の概要①
本論文は主に”MNARデータを使ったオフライン評価”に焦点を当ててる(“学習”にも一般化可能). MNARデータ \(D_{mnar}\) からサンプリングしてMARデータ \(D_{mar}\) に近い性質を持つ介入データ \(D_{S}\) を作る、新しいサンプリング戦略を提案している.
MARデータとMNARデータが満たすべき性質の違いを、観測された{u,i}ペアの事後確率 \(P(u,i|\mathcal{O} = 1) = P(u,i|\mathcal{O})\) の観点から以下の様に定義する:
\[
P_{mar}(u,i|\mathcal{O}) = P_{mar}(u|\mathcal{O}) \cdot P_{mar}(i|\mathcal{O}) \approx \frac{1}{|U|} \cdot \frac{1}{|I|} = \frac{1}{|U||I|}, \forall(u,i) \in U \times I
\]
\[
P_{mnar}(u,i|\mathcal{O}) \neq P_{mnar}(u|\mathcal{O}) \cdot P_{mnar}(i|\mathcal{O}), \forall (u,i) \in U \times I
\]
ここで、\(\mathcal{O}\) は “観測されたか否か”を表すbinary確率変数.
提案手法の概要②
- サンプリング戦略 \(S\) は確率分布関数 \(P_S(\mathcal{S}=1|u,i), \forall(u,i) \in D_{mnar}\) に基づいて実行される. ここで、\(\mathcal{S}\)は\(D_{mnar}\) 中の任意の{u,i}ペアをサンプリングするか否かを表すbinary確率変数. (i.e. {u,i}を条件づけた時に \(\mathcal{S} = 1\) となる確率が決定される関数のイメージ 🤔)
- 提案手法のアイデアは、介入データ \(D_S\) 中の{u,i}事後確率分布 \(P_S(u，i|\mathcal{S})\) を\(P_{mar}(u, i|\mathcal{O})\) と同じにする事.(i.e. MARデータに後付けで似せたい🤔)
- ２つのサンプリング戦略 WTD (少量のMARデータが必要ver.)と WTD_H (少量のMARデータが不要ver.).
提案手法の概要③
サンプリング用のユーザ重み \(w_u\) とアイテム重み \(w_i\) を以下の様に定義.
\[
w_{u} = \frac{P_{mar}(u｜\mathcal{O})}{P_{mnar}(u｜\mathcal{O})},
w_{i} = \frac{P_{mar}(i｜\mathcal{O})}{P_{mnar}(i｜\mathcal{O})}
\]
重みを使って以下のサンプリング確率分布関数をモデル化: (サンプリングにおける重みの効果は、サンプリング空間のMNAR分布とMAR分布がどれだけ乖離してるかに基づいて、{u,i}ペアのサンプリング確率が増減すること)
\[
P_S(\mathcal{S}|u,i) = w_u \cdot w_i
\\
\text{実際には経験的にこっちを採用:} P_S(\mathcal{S}|u,i) = w_u \cdot (w_i)^2
\]
\(P_{mar}(u,i|\mathcal{O})\) に関して、観測値から推定する場合は本戦略を WTD と呼び、仮説のMAR事後分布(i.e. \(P_{mar}(u|\mathcal{O}) = 1/|U|, P_{mar}(i|\mathcal{O}) = 1/|I|\))を用いる場合は WTD_H と呼ぶ.
実験結果の概要① モデル精度指標のground-truth との差
表2は、各推薦モデルに関するオフライン評価精度(Recall@10)のにおいて、ground-truth(=MARテストセットによる評価結果)と各サンプリング戦略による介在テストセットによる推定値の差を表したもの.
![]()
- 提案手法(WTD, WTD_H)は、ground-truthのモデル性能を最も良く近似できている.
- FULL戦略(\(D_{mnar}\)そのまま使う戦略)とREG戦略(\(D_{mnar}\)からランダムサンプリングする戦略)の結果は似ておりground-truthから非常に離れている. -> debias効果に重要なのは”サンプリングする事”そのものではなく、“いかにサンプリングするか”という戦略である.
最後に…読んだ感想
- 実務において、推薦モデルのオフライン評価では良いモデルと判断したのに、実プロダクトに組み込んだオンライン評価(ABテスト)ではイマイチ、というケースに遭遇したので、何とか改善できればと思っている.
- 論文1と論文2で提案された手法はどちらも、“学習”と”オフライン評価”の両方に適用可能であり、またモデルフリーというかMLモデルの種類に依存せず適用可能な点は好印象…!
- 導入時の開発コスト的には、論文2のサンプリングアプローチの方が容易そう.(論文1の手法ではPropensity scoreを推定するプロセスを追加する必要があるので…)
- 今回の内容は”オフラインでの精度評価を正しく推定しよう”というモチベーションの話だが、これだけでオフライン評価-オンライン評価の乖離が必ずしも埋まるとは限らないと思っている.
- オフライン評価可能なmetrics と オンライン評価値の両方をモニタリングして、それらの相関関係を見たり回帰モデルを推定したりする試みもあるので、実務での運用を検討してみたい.( 参考論文)
参考文献
